CS231n Lecture3 정리

Lecture3 : Loss Functions and Optimization

Linear classification의 기본 (Loss function, Optimization)을 다루고, Loss function의 예시로 Multiclass SVM과 Softmax, Optimization의 예시로 Stochastic Gradient Descent(SGD) 에 대하여 설명한다.

Linear Classifier의 개요

다음과 같은 Parametric Approach를 생각해보자.

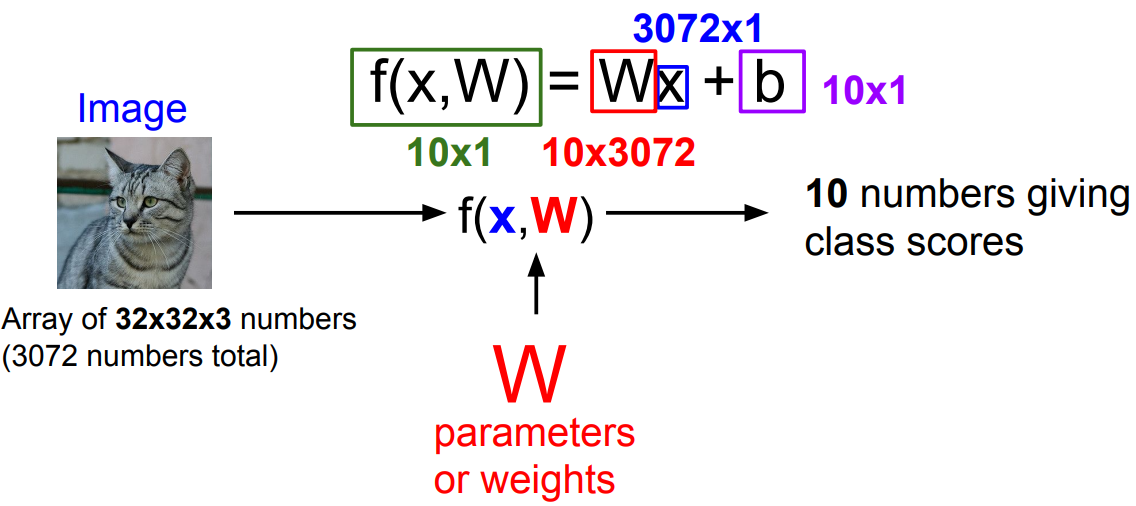
$f(x, W) = Wx + b$의 형태로, $W$와 $b$를 정해주면 image $x$를 input으로 하였을 때 $f(x, W)$가 추측된 label을 알려준다.

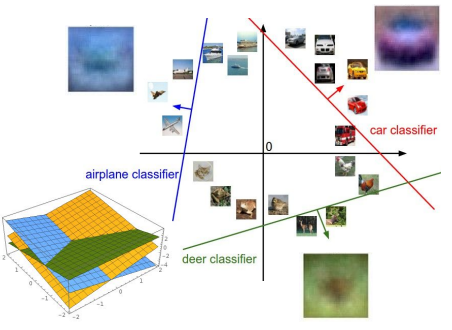
다음의 두 가지를 염두해야 한다.

1. Loss function을 정의하여 모델의 “어긋난 정도”를 파악할 방법을 마련해야 한다.
2. optimization: 정의한 loss function을 최소화할 수 있는 parameter를 효율적으로 찾는 방법을 마련해야 한다.

Loss function : 모델의 분류 성능을 대변한다

$x_i$가 image, $y_i$가 label(integer) 라고 할 때 ${\{(x_i, y_i)}\}_{i=1}^{N}$ 의 example dataset이 주어진다. Total Loss $L$은 각 이미지의 loss를 모두 더한 것과 같다.

$$L = {1 \over N} \sum_{i}L_i(f(x_i, W), y_i)$$

Multiclass SVM loss

score vector $s = f(x_i, W)$ 와 같이 정의할 때, SVM loss는 다음과 같이 정의한다.

$$L_i = \sum_{j \neq y_i} \begin{cases} 0 & \text{if} \enspace s_{y_i} \geq s_j + 1 \\ s_j - s_{y_i} + 1 & \text{otherwise} \end{cases} \\[2em] = \sum_{j \neq y_i} \text{max}(0, s_j - s_{y_i}+1)$$

• Possible min/max loss : 0, $ \infty $
• Debugging strategy: 초기에 $W$가 매우 작아 모든 $s \approx 0 $ 일 때, $\text{loss} = \text{num of classes} - 1 $

Regularization

• Training Data에 overfit되는 것을 방지하기 위하여, 다음과 같이 Regularization term을 추가해 준다: (SVM의 예시) $$L = {1 \over N} \sum_{i}L_i(f(x_i, W), y_i) + \lambda R(W)$$
• Train data에서는 오차가 조금 더 생기겠지만, 모든 data(Test data)에 대해서는 더 좋은 model이 되기 위한 penalty라고 생각할 수 있다.
• 여기서 $\lambda$는 hyperparameter 이다.
• 가장 흔한 방법은 L2 regularization이다. $$R(W) = \sum_k \sum_l W_{k,l}^2$$

Softmax Loss

Softmax loss는 다음과 같이 정의한다.

$$L_i = -\log {e^{s_k} \over \sum_j e^{s_j}}$$

• Possible min/max loss : 0, $ \infty $ (둘 다 이상적인 경우임)
• Debugging strategy: 초기에 $W$가 매우 작아 모든 $s \approx 0 $ 일 때, $ \text{loss} = \log(\text{number of classes}) $

SVM과 Softmax의 비교

• SVM: 판별 자체에 중점을 두고, 그 이후는 관여하지 않음
• Softmax: 더 정확하게 (독보적인 선택으로; 깔끔하게) 판별하는 것을 신경씀
• 따라서 한 Datapoint를 아주 조금 바꾸었을 때, SVM은 loss 값이 바뀌지 않을 수 있지만 Softmax는 반드시 바뀜

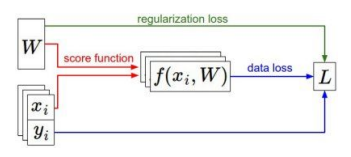
Optimization: 최고의 $W$ 찾기

Loss값을 가장 빠르게 최소화하는 방향(direction of steepest descent) 이 negative gradient 임을 이용한다!

Numerical Gradient

미분의 정의를 이용하여 수학적으로 직접 계산한다.

$${df(x) \over dx} = \lim_{h \to 0} {f(x+h) - f(x) \over h}$$

$h$를 아주 작은 0.0001 정도로 두고 각 항을 직접 loop을 돌며 계산할 수 있지만, 너무 느리다

Analytic Gradient

Calculus를 이용하여, 직접 $ \nabla_WL $ 을 수학적으로 계산한다!

Gradient 구하기 결론

항상 Analytic Gradient를 이용하지만, Numerical Gradient를 이용하여 확인해볼 수 있다. ( gradient check )

Gradient Descent

negative gradient가 가장 급격하게 감소하는 방향임을 이용하여, 조금씩 움직이면서 반복한다.

while True:
  weights_grad = evaluate_gradient(loss_func, data, weights)
  weights += - step_size * weights_grad

여기서 step_size는 hyperparameter인데, 생각보다 꽤 중요하다고 한다.

Stochastic Gradient Descent (SGD)

전체 Sum을 계산하는 것은 굉장히 expensive 하므로, minibatch 를 이용하여 작은 data만 이용하여 Gradient Descent를 적용한다.,

while True:
  data_batch = sample_training_data(data, 256) # 256개의 data만 사용
  weights_grad = evaluate_gradient(loss_func, data_batch, weights)
  weights += - step_size * weights_grad