ReLU, Affine 계층에서의 Backpropagation

CS231n assignment1 two_layer_net.ipynb 의 구조는 input - fully connected layer - ReLU - fully connected layer - softmax 로 이루어진다. (neural_net.py 참고) 등장하는 ReLU 계층, Affine 계층을 Lecture 4에 소개했듯 modularization 하여 정리해 보려고 한다.

ReLU 계층

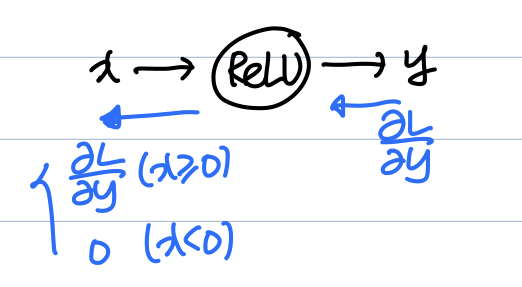
ReLU function의 형태는 다음과 같다.

$$y = \begin{cases} x & \enspace (x \geq 0) \\ 0 & \enspace (x < 0) \end{cases}$$

따라서 $x$로 편미분 하면 다음과 같다.

$${\partial y \over \partial x} = \begin{cases} 1 & \enspace (x \geq 0) \\ 0 & \enspace (x < 0) \end{cases}$$

즉, Backpropagation 결과는 다음과 같다.

$${\partial L \over \partial x} = \begin{cases} {\partial L \over \partial y} & \enspace (x \geq 0) \\ 0 & \enspace (x < 0) \end{cases}$$

Affine 계층

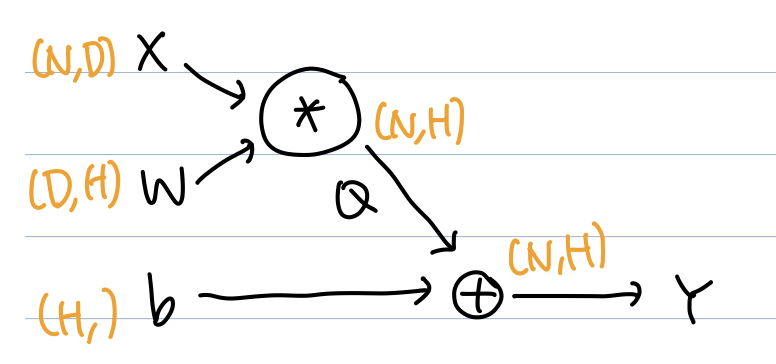
Affine 계층이란 Neural Network에서의 fully-connected layer를 의미한다. 본 과제에서는 $X$가 $(N, D)$ 의 행렬의 형태로써 다음과 같이 vectorized된 형태를 제시한다.

$$Y = X \cdot W + b$$

이를 computational graph로 표현하면 다음과 같다.

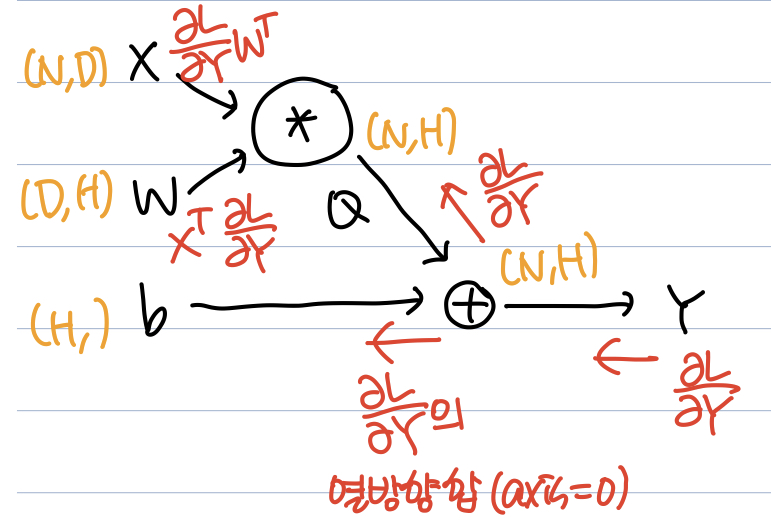
Lecture 4 에서 add gate 가 gradient distributor의 역할을 한다 하였고, Backpropagation for a Linear Layer 를 이용하면 ${\partial L \over \partial X}$ 와 ${\partial L \over \partial W}$ 는 쉽게 구할 수 있다. 문제는 ${\partial L \over \partial b}$ 인데, 결과론적으론 다음을 얻는다.

$${\partial L \over \partial X} = {\partial L \over \partial Y} \cdot W^T$$ $${\partial L \over \partial W} = X^T \cdot {\partial L \over \partial Y}$$ $${\partial L \over \partial b} = {\partial L \over \partial Y}.\text{sum(axis = 0)}$$

즉, ${\partial L \over \partial b}$ 는 ${\partial L \over \partial Y}$ 의 row 방향 합(axis = 0)이다. 일단 shape의 측면에선 맞아 떨어지는데, 어떻게 이를 해석할 수 있는지 생각해보자. Affine 계층에서 $Y = X \cdot W + b$ 가 되면 $b$ 가 broadcasting 되어 모든 row에 더해진다. 쉽게 생각하였을 때 ${\partial L \over \partial b}$ 는 $b$ 가 $L$ 에 미치는 영향을 의미한다. $b$ 가 모든 row에 더해졌으므로 $b$ 가 $L$ 에 미치는 전체 영향을 구하려면 편미분 값을 row 방향으로 합쳐서 모두 더해주어야 하지 않겠는가?

최종적으로 gradient를 표시한 computational graph는 다음과 같다.

위의 수학적 계산 결과를 알고 있다면, CS231n assignment1의 two_layer_net.ipynb 는 매우 쉽게 해결할 수 있다.