Lecture 5 : Convolutional Neural Networks

CNN의 기본 원리와 용어 설명에 대하여 설명한다. Channel(Depth), Filter, Stride, Padding, Pooling Layer 를 다룬다.

CNN 기본 원리

Channel (Depth)

CNN의 특징은 이미지의 spatial structure를 유지한다는 것이다. (기존의 Fully Connected Network에서는 한 이미지당 한 개의 긴 row vector로 늘렸었다.) 이미지의 크기가 $ H \times W \times C $ 라고 하자. 여기서 $C$ 는 channel 을 의미하며, 사용된 색의 개수로 쉽게 이해할 수 있다. 컬러 이미지는 RGB의 세 가지 색을 이용하므로 channel = 3 이며, 흑백 이미지는 channel = 1 이다. Depth로 불리기도 한다.

Filter

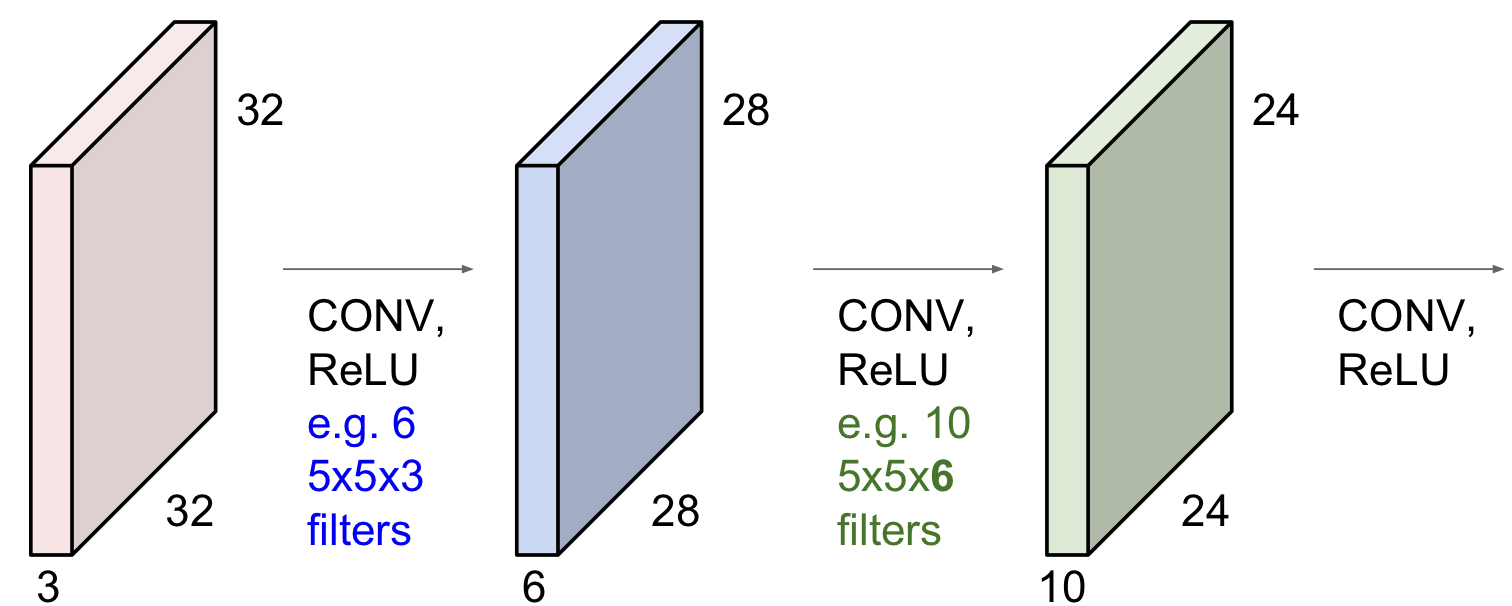
이제, 이 이미지가 $ HH \times WW \times C $ 의 크기인 filter로 연산 된다. 실제 convolution 연산과 유사하게 (단, filter 반전은 없다) 이미지에서 filter의 크기와 같은 영역이 filter와 모두 곱해져 하나의 scalar로 계산된다. 이러기 위해서는 이미지의 depth와 filter의 depth가 같아야 한다. 필터가 $F \times F$의 size라면, 필터의 크기를 $F$ 라고 한다.

한 개의 filter는 한 개의 2D output을 만든다. $K$개의 filter가 있으면, depth가 $K$인 3D array가 output이 된다. 주로 $K$는 2의 거듭제곱 꼴로 둔다.

Stride

stride란, filter와 이미지가 합성곱 될 때 filter가 한 번에 이동할 칸 수이다. 합성곱 연산을 진행하게 되면 이미지의 크기가 계속 감소하는데, 이는 어찌보면 정보를 잃는 과정이므로 이를 보완하기 위해 padding 작업을 해준다.

Padding

padding 이란 이미지의 주변에 새로 data를 붙여주는 것을 의미한다. 가장 대중적인 방법은 zero padding 인데, P개의 줄만큼 이미지의 주변에 0을 추가로 붙여준다. filter의 크기가 $ F \times F $ 일 때, $ P = {F-1 \over 2} $ 로 padding을 두면 연산을 해도 이미지의 크기가 보존된다.

최종적인 연산 결과

• 이미지의 크기: $ H \times W \times D $
• 필터 개수: $K$
• 필터의 크기: $F$
• Stride: $S$
• Zero padding: $P$

의 값들로 연산된 output은 다음과 같은 $ H_2 \times W_2 \times D_2 $ 의 크기를 가진다:

• $ H_2 = {H - F + 2P \over S} + 1 $

• $ W_2 = {W - F + 2P \over S} + 1 $

• $ D_2 = K $

  

Pooling Layer

Pooling Layer는 depth의 변화 없이 output의 사이즈를 줄이기 위해 사용한다. 일종의 downsampling이라 생각하면 된다. 가장 유명한 Max Pooling은 Filter의 크기 안에서 가장 큰 값만 선택하여 남긴다. Activate하는 놈을 강조(특징 살리기)한다는 입장에서 보면,이 과정이 정당하다고 받아들일 수 있다.

Pooling Layer에서는 보통 zero-padding을 사용하지 않는다. 따라서 $ H \times W \times D $ 의 이미지를 크기 $F$, stride $S$의 pooling filter로 max pooling 하면 $ ({H - F \over S} + 1 )\times ({W - F \over S} + 1 )\times D$ 의 output이 나온다.

Typical Architectures

전형적인 구조는 아래와 같다.

$$[ (CONV - RELU)\times N - POOL]\times M - (FC - RELU) \times K - SOFTMAX$$